Линейное программирование

Под линейным программированием, также известным как линейная оптимизация, понимается метод определения наилучшего результата, получаемого с использованием линейной математической модели и задания множества ограничений.

Этот инструмент позволяет решать проблемы, связанные с минимизацией и максимизацией задаваемых условий, например достижения максимальной прибыли при минимальных затратах. Так, вводя ограничения на количество материалов и затраты труда, вы могли бы использовать линейное программирование для определения «лучшего» уровня производства, позволяющего добиться максимальной прибыли в этих условиях.

Первоначально он был разработан в 1937 г. Леонидом Канторовичем и во время Второй мировой войны применялся как способ планирования расходов и результатов, позволяющий, с одной стороны, сократить затраты на армию, а с другой — добиваться максимальных потерь у врага. Метод держался в секрете до 1947 г. — именно в этот год Джордж Данциг в значительной степени его упростил, после чего он стал применяться не только для военных целей.

В настоящее время линейное программирование широко используется в различных областях, включая бизнес, экономику и инженерное дело, для поиска оптимального решения при наличии различных линейных соотношений и ограничений.

Содержание

Когда следует применять инструмент

Линейное программирование является частью очень важной и полезной области математики, называемой методами оптимизации. Очевидно, возможность оптимизировать свои ресурсы является одним из важных умений, помогающим добиваться успеха не только в бизнесе, но и в других сферах. Вы можете прибегнуть к этому инструменту, если у вас есть ряд ограничений, например по времени, сырью, числу работников, марже прибыли, и вы хотите узнать, какая комбинация составляющих является лучшей или куда следует направить свои ресурсы для получения максимальной прибыли.

По существу, линейное программирование является процессом распределения ресурсов, результаты которого могут помочь принимать более обоснованные решения и повысить доход.

С его помощью можно промоделировать множество задач различных типов, таких как планирование, маршрутизация, распределение ресурсов и проектирование.

К числу отраслей, в которых используется этот инструмент, относятся, помимо прочих, транспортная, энергетическая, телекоммуникационная и производственная.

Вопросы, на которые можно получить ответ с помощью инструмента

Линейное программирование может помочь вам решить, как лучше распределить ваши ресурсы, чтобы добиться результатов, максимально возможных в имеющихся условиях. В частности, оно позволит вам ответить на следующие и им подобные вопросы.

Как я могу наилучшим образом распределить ресурсы, чтобы оптимизировать процессы?
Как мне лучше всего использовать ресурсы, чтобы добиться максимальной прибыли?
Какой маршрут доставки, учитывая наши ограничения, является оптимальным?
Каковы оптимальные затраты сил, позволяющие получить на выходе максимальный объем продукции?

Как следует пользоваться инструментом

Первым шагом при применении линейного программирования является определение ваших контрольных переменных (обычно обозначаемых х и у). Затем нужно задать целевую функцию, т. е. определить, что именно вы пытаетесь максимизировать или минимизировать. После этого нужно в виде неравенств ввести ограничения, относящиеся к контрольным переменным. И, наконец, сформулированную задачу следует решить графически.

Полученный график в наглядном виде представляет неравенства, которые в совокупности на плоскости, заданной координатами х и у, образуют «огороженную» зону. Эта зона называется «областью допустимых решений»; ее положение на графике позволяет определить координаты углов этой области.

Это делается путем нахождения точек пересечения различных пар применяемых линий. После их определения вы можете проверить эти угловые точки с помощью уравнения оптимизации, чтобы найти ту, которая имеет наибольшее или наименьшее значение.

Если вы хотите узнать больше о линейном программировании и о том, как следует пользоваться этим инструментом, обратитесь к поисковым системам, или воспользуйтесь соответствующими инструментами программного обеспечения, которые могут вам помочь.

Практический пример

Следующий пример и графики были взяты по ссылке http://www. thestudentroom.со.Uk/wiki/revision:linear_programming. Допустим, вы руководите заводом, на котором производятся два основных изделия — продукт х и продукт у. Однако у вас столько производственных линий и людей, работающих на них, что каждый раз завод может производить лишь один продукт. Число имеющихся у вас работников и продолжительность их труда при производстве любого из двух продуктов одинаковы, то же самое верно и в отношении ресурсов, используемых для производства каждого из них, а вот цена продажи единицы каждого продукта и число продаваемых единиц разные.

Вы пока до конца не разобрались в том, как вам следует распределять различные ресурсы, имеющиеся на вашем заводе. Вы можете использовать свой опыт и изучить прошлые данные. В этом есть смысл, но вы не можете избавиться от ощущения, что должен быть более подходящий способ решения этой задачи, и поэтому вы решили прибегнуть к линейному программированию, чтобы его результаты помогли вам в процессе принятия решений.

Контролируемыми переменными в вашем случае являются продукты х и у, а. целевая функция формулируется так: выяснить, как можно максимизировать прибыль. Вы определили, что у вас имеются следующие ограничения:

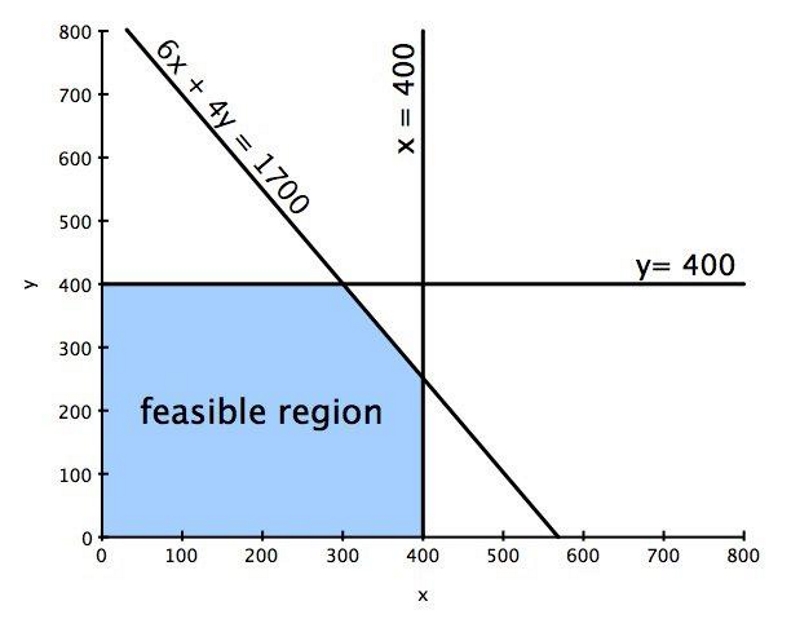
для производства единицы продукта х, реализация которого приносит 12 условных единиц прибыли, нужно 6 ч; для производства единицы продукта у, реализация которого приносит 6 условных единиц прибыли, нужно 4 ч;
из-за различных ограничений завод может произвести максимум 400 единиц любого продукта;
всего на производство продуктов вы можете выделить 1700 ч.

Получившаяся в конечном счете область допустимых решений показана на следующем графике.

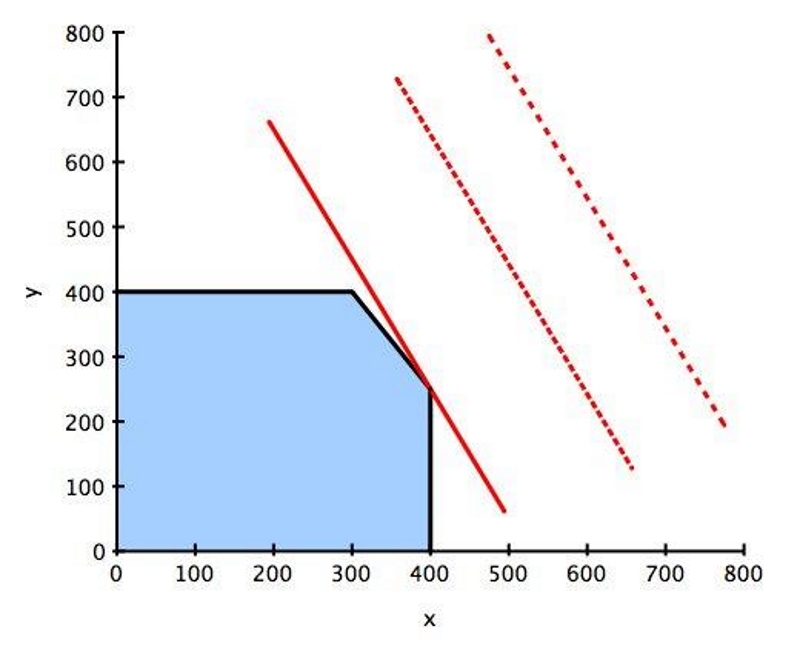
Вы знаете, что прибыль является максимальной в одном из углов этой области. Чтобы определить, в каком именно, проведите линию с таким же наклоном, как у целевой функции, и переместите эту линию ближе к области допустимых решений. Прибыль будет максимальной в том ее угле, которого эта линия коснется первой.

На втором графике линия целевой функции касается области допустимых решений в угловой точке с координатами 400 и 250.

Это означает, что для получения максимальной прибыли с имеющимися у вас ресурсами вам необходимо произвести 400 единиц продукта х и 250 единиц продукта у, в результате чего вы получите прибыль в размере 6300.

О чем не нужно забывать

В производственном процессе очень легко возникают самые разные узкие места, из-за чего всегда приходится выяснять, как лучше всего в возникшей ситуации использовать имеющиеся у вас ресурсы. Если вы не будете внимательно отслеживать ход производства, одни виды оборудования могут простаивать, в то время как другие работать с перегрузкой. Линейное программирование может помочь вам выявить подобные проблемы и наилучшим образом использовать большую часть имеющихся у вас ресурсов.

Конечно, сказанное по-настоящему полезно только для тех задач, которые можно выразить в виде линейных уравнений (графически представленных прямой линией). Не все ограничения являются полезными, так как в некоторых таких случаях воспользоваться линейным программированием не удастся. К тому же всегда есть и другие факторы, которые вам, возможно, придется принять во внимание, такие как погодные условия или более широкие рыночные условия. Используйте линейное программирование как инструмент для принятия решений, но не полагайтесь полностью на полученные с его помощью результаты без учета того, как на эти результаты могли повлиять другие неопределенные факторы.